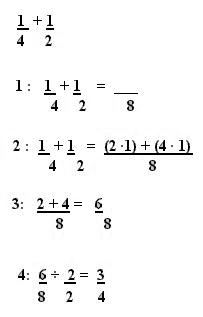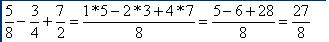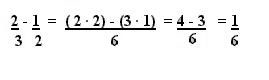JUGAMOS CON LAS FRACCIONES
HAS CLIC EN LAS IMÁGENES.
Fracciones
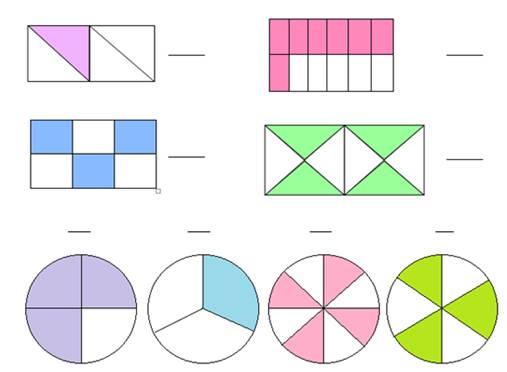
Una fracción es una parte de un total
Corta una pizza en trozos, y tendrás fracciones:
 |
 |
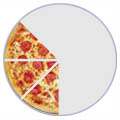 |
| 1/2 |
1/4 |
3/8 |
|
(Una mitad)
|
(Un cuarto)
|
(Tres octavos)
|
| |
|
|
| El número de arriba te dice cuántas porciones tienes y el de abajo te dice en cuántos trozos se ha cortado la pizza. |
Numerador / Denominador
Al número de arriba lo llamamos
Numerador, es el número de partes que tienes.
Al de abajo lo llamamos
Denominador, es el número de partes en que se ha dividido el total.
¡Sólo tienes que recordar esos nombres! (Si los confundes, recuerda que denominador es con "D" de dividir)
Fracciones equivalentes
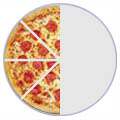
Algnas fracciones parecen diferentes pero en realidad son la misma, por ejemplo:
| |
4/8 |
= |
2/4 |
= |
1/2 |
|
|
(Cuatro octavos) |
|
(Dos cuartos) |
|
(Una mitad) |
|
| |
 |
|
 |
|
 |
|
Normalmente lo mejor es dar la respuesta usando la fracción más simple (
1/2 en este caso).
Eso se llama
Simplificar o
Reducir la fracción.
Sumar fracciones
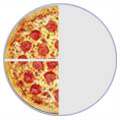
Puedes sumar fracciones fácilmente si el número de abajo (el
denominador) es el mismo:
| |
1/4 |
+ |
1/4 |
= |
2/4 |
= |
1/2 |
|
| |
(Un cuarto) |
|
(Un cuarto) |
|
(Dos cuartos) |
|
(Una mitad) |
|
| |
 |
|
 |
|
 |
|
 |
|
Otro ejemplo:
Sumar fracciones con denominadores diferentes
¿Y si los
denominadores no son iguales? Como en este ejemplo:
Deberías hacer que los denominadores fueran iguales
de alguna manera. En este caso es fácil, porque sabemos que
1/4
es lo mismo que
2/8 :
En ese ejemplo fue fácil hacer que los denominadores fueran el
mismo, pero puede ser más difícil... visita las páginas de los métodos
de
ADICIÓN DE FRACCIONES CON DIFERENTE DENOMINADOR:
Diremos
que dos fracciones son heterogéneas cuando estas poseen distinto
denominador, por lo cual se diferencian de las fracciones homogéneas,
que tienen el denominador en común. Si lo que queremos es realizar sumas
o restas con fracciones heterogéneas lo que debemos hacer en primer
lugar, es encontrar el común denominador, o sea hallar el mínimo común
múltiplo de todos los denominadores. Luego de esto lo que se debe hacer
es colocar el denominador común, dividimos entonces el común denominador
entre el primer denominador y el resultado lo multiplicamos por el
numerador. Repetimos la operación con cada una de las fracciones que
tengamos. Por último se suman los resultados obtenidos y así
finalizamos. A veces no es necesario multiplicar entre si los
denominadores, eso depende de las fracciones que tengamos. Veamos ahora
un ejemplo de suma de fracciones heterogéneas bastante sencillo:

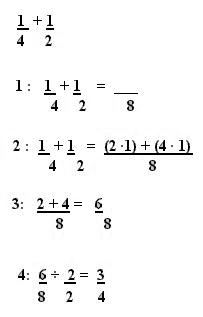
Vemos en el ejemplo anterior que en primer lugar se multiplicaron los
denominadores, luego se realizó la multiplicación cruzada. Se sumaron
los productos para obtener luego el numerador y finalmente se simplificó
la fracción. Observemos otro ejemplo:
Podemos observar en este ejemplo que no fue necesario multiplicar entre
si los denominadores, ya que 8 es múltiplo común tanto de 2 como de 4
así como de si mismo.
En la resta o sustracción de fracciones heterogéneas debemos utilizar
las mismas reglas que usamos en la suma, lo único que cambia es que en
este caso tenemos que restar en vez de sumar. Veamos un ejemplo:
Pasos para resolver los fraccionarios con diferente denominador sencillos:
1. Halla el máximo común múltiplo de los denominadores:
2. Complica ambas fracciones:
3. suma las fracciones.
4. suma las fracciones complificadas.
La suma de fracciones está basada en la ley fundamental de la suma que
dice que "solamente cosas iguales se pueden sumar y el resultado debe
ser de esas mismas cosas". O sea que cosas diferentes no se pueden
sumar. Es de sentido común que no se pueden sumar cuadernos más libros.
Además, que si se suman esferos más esferos el resultado son esferos, no
camiones. Por esa razón, de entrada no se puede sumar un medio más un
tercio porque son cosas diferentes: la primera son mitades y la otra son
terceras partes, que al final de cuentas son cosas diferentes. Para
poder efectuar esta suma, la Aritmética hace un truco muy simple para
reducir ambas fracciones a "cosas iguales" (fracciones equivalentes).

Proceso para sumar o restar fracciones heterogéneas usando el método de multiplicación cruzada (puedes usarlo solo cuando trabajas con dos fracciones)
v Multiplicas los denominadores, ahora ese será el denominador de la nueva fracción.
v Multiplicas
el numerador de la primera fracción por el denominador de la segunda
fracción y lo escribes en el numerador de la nueva fracción.
v Escribe en la nueva fracción el símbolo de la operación matemática que estas trabajando.
v Multiplicas
el numerador de la segunda fracción por el denominador de la primera
fracción y lo escribes en el numerador de la nueva fracción (después del
símbolo de operación matemática).
v Suma o resta los numeradores.
v Simplifica tu respuesta.
 JUGAMOS E IMPRIMIMOS PARA SEGUIR MEJORANDO CON LAS FRACCIONES
JUGAMOS E IMPRIMIMOS PARA SEGUIR MEJORANDO CON LAS FRACCIONES